One-Hot encoding

Categorical variable

Do you know what a categorical variable is ? If you do not know it, you have certainly encountered the concerns that this type of characteristic imposes with regard to Machine Learning algorithms. To put it simply, this type of characteristic is not quantitative (ordinal variable). It is therefore not digital (well in the majority of cases) but offers equally important qualitative information.

Your challenge as a Data Scientist is to convert this qualitative into quantitative!

However, the thing is not easy because to convert qualitative it is necessary to know its value and to be able to scale it in relation to the other available data. A case-by-case approach seems necessary, but other, simpler techniques can help you move forward.

One-hot encoding

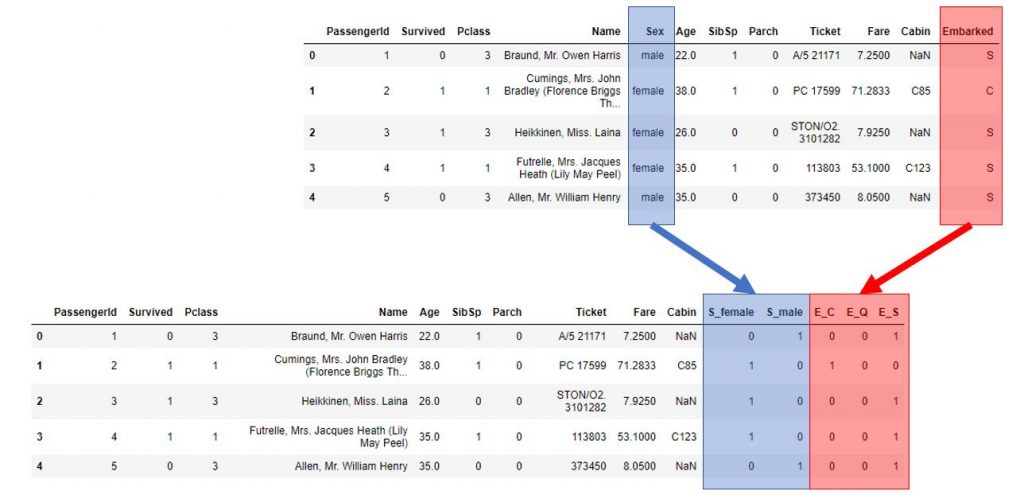
This is the easiest method. The one that you will often use above all else. The idea is very simple: create and add binary columns (dummies) which refer or not to the data by a 0 or 1. Take for example the titanic dataset, you have columns which contain categorical variables like Gender, Cabin , etc. The idea is to add additional columns to the data set by specifying in relation to each data if it exists or not.

The example of Sex is rather telling. In the dataset this categorical variable takes only two values ​​male and female. We will therefore replace this column (with two values) by two columns male and female.

You can check it simply with the Pandas library as follows:

display(titanic.columns)
cols = ['Sex', 'Embarked']
for col in cols:
    display('Colonne: ' + col)
    display(titanic[col].value_counts())

Note: I added the Embarked categorical variable to this to refine the future model.

Fortunately the Pandas library comes to our rescue once again and creates the famous dummies columns for us in no time at all (thanks to the get_dummies method):

data_dummies = pd.get_dummies(titanic, prefix=['S', 'E'], columns=['Sex', 'Embarked'])
display(data_dummies.columns)
data_dummies.head(5)

Here is the result :

Some limits

Have you not wondered why you didn’t take the Cabin column or even the Name column? and quite simply because these columns present too many values ​​on their distribution. Indeed, adding dummies columns would risk adding almost as many columns as there are existing rows! (this is especially true for the name) and therefore no interest for the rest of the treatments.

An intermediate solution will require us to dissect the data in order to group them into larger clusters. This will allow us to apply the previous method to it.

For the Name column, why not split (parse) this name and get the last name there. Will the frequency of distribution of surnames make it possible to create a sufficient group? For the Cabin column, why not parse / retrieve the first letter? It is very likely that the first letter corresponds to a deck of the boat for example, right?

Let’s try this with Pandas. Let’s first look at the distribution of this characteristic:

display(titanic['Cabin'].value_counts())

We get 147 possible values ​​on this test set.
Be careful because we have unspecified values ​​(NaN), which must be filled for this parameter, why not add (for the moment a fictitious bridge X)??

cabin = titanic['Cabin'].fillna('X')
display(cabin.value_counts())

Obviously we now have 148 distinct values.

Now let’s take only the first character of the cabin:

display(cabin.str[0].value_counts())

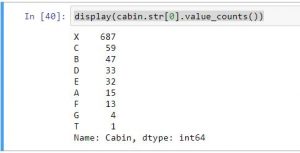
t’s much better we only have 9 possible values!

Why not add this new column (Bridge?) And turn it into dummie columns (9) now?

Another concern that you may encounter is when your categorical variable is of numeric type. This happens often in fact and in this case scikit-learn offers you the OneHotEncoder class to handle this scenario.

Let’s apply our work with a logistic regression

First, let’s prepare the data so we don’t forget to provide only numeric data to our logistic regression algorithm (on titanic data):

from sklearn.linear_model import LogisticRegression
lr1 = LogisticRegression()
def Prepare_Modele(X, cabin):
    target = X.Survived
    sexe = pd.get_dummies(X['Sex'], prefix='sex')
    cabin = pd.get_dummies(cabin.str[0], prefix='Cabin')
    age = X['Age'].fillna(X['Age'].mean())
    X = X[['Pclass', 'SibSp']].join(cabin).join(sexe).join(age)
    return X, target
X, y = Prepare_Modele(titanic, cabin)
lr1.fit(X, y)
lr1.score(X, y)

We get a score of 81%

The conclusion is that there is no miracle recipe when it comes to dealing with categorical variables. Very often it is here that business knowledge is essential in order to better understand and manage these characteristics.