Markov chains

Introduction

Markov chains have been somewhat neglected since the appearance of Machine Learning algorithms. However, they are still quite used, especially for weather forecasts and even for completion when you do a search in Google.

The philosophy as well as the implementation are indeed quite simple. We will see in this article on an extremely simple case how to model this type of algorithm but also how to use it with Python.

First of all, no need to start with large mathematical equations first. The idea of ​​Markov chains is to first describe a state sequence. For the weather, for example, we will make a series of observations such as:

• D + 0: Good weather
• D + 1: Rain
• D + 2: Rain
• D + 3: Good weather
• etc.
• D + n: Cloudy

This series of findings is a sequence, each step of a sequence indicates a state. With Markov chains, we will first draw this observation. The idea is very simple, starting from one or more observations we will define the transition probabilities between each state. These mapped and referenced probabilities will then allow us to define our forecasts. Simple isn’t it? let’s see what that will give on a concrete case.

Concrete case: The positions of the cat!

Let’s change the subject (weather) and do an experiment together. Imagine that we look at our cat and that every 5 minutes we note his posture. This could give this sequence of observations:

1. Minute 0 : Standing (Debout in french below ;-))
2. Minute 5: Sitting (Assis which means sitting)
3. Minute 10: Sitting
4. etc.
5. Minute 40: Sitting

Note: in the schema below “Couché” means Lying.

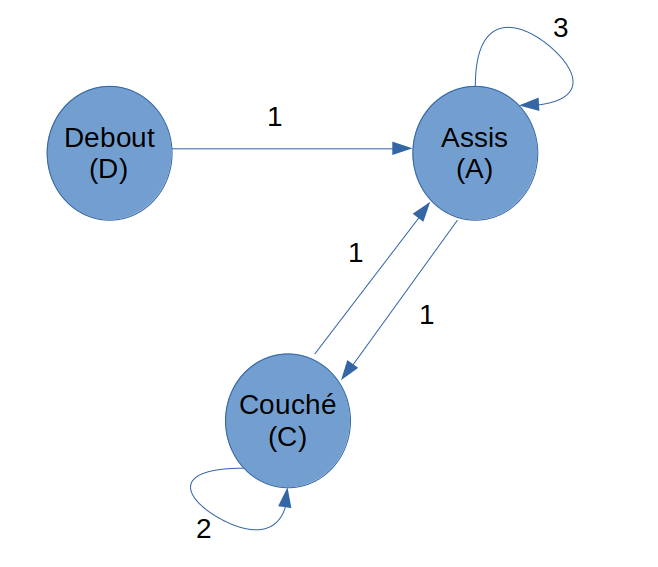
From a sequential point of view it could be presented like this:

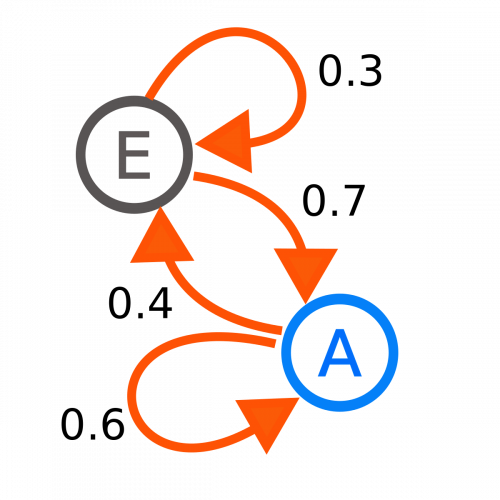
What is interesting now is to show this same sequence from the angle of states. For that we will create a circle for each state and we will connect these states in relation to those observed in our sequence:

Great to see thaks to that’s diagram how it is easy to look at and understand the global process just because there is no more state redundancy.

An important characteristic of Markov chains is that their principle is based on a state and not on a state history. A Markov chain is a series of random variables: the future does not depend on the past, or in other words the future depends on the past only through the present.

Another important point is that Markov chains are based on probabilities. The idea is to define a probability matrix (called the transition matrix) which will allow us to calculate a forecast on the following steps.

Let’s calculate the probabilities of our cat’s positions

It’s very simple actually. In the following diagram we note the probability of the passage from state C (lying down) to state D (Standing) in this way:

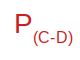
This probability is called the transition probability of a process step.

Compared to the possibilities observed during the experiment, we will have the following probabilities:

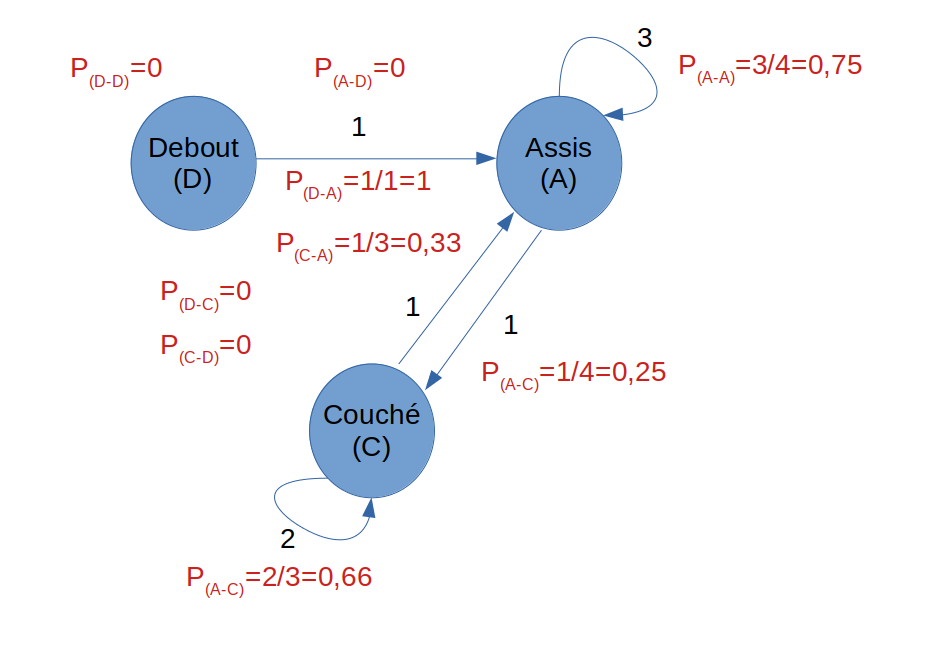
For example: The probability of going from the lying state (C) to the sitting state (A) is 2 in 3 (or 0.66). We have indeed 2 arrows which loop on state C and an arrow which goes towards A: that is to say 3 possibilities in total of change of state.

The transition matrix

Once all the state change probabilities have been defined / calculated, they can be represented in the form of a matrix (Transition matrix). We will have a 3 × 3 square matrix because we have 3 states that we will write as follows:

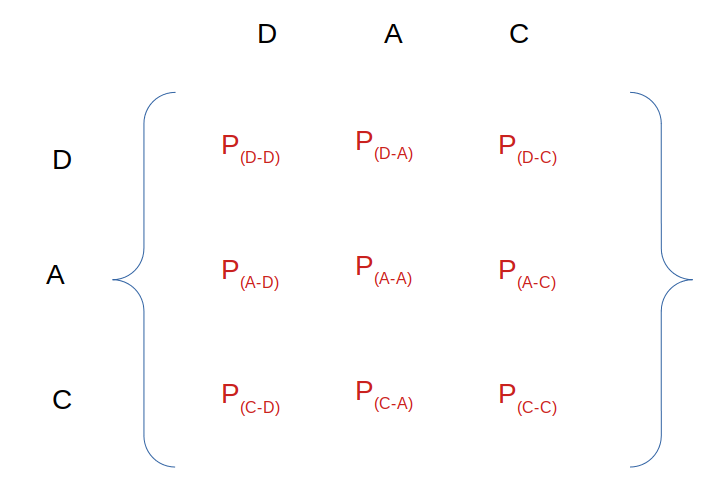
Consider the following digital matrix:

This matrix will allow us to simply calculate the forecast of passage from a stage 1 to a stage 2. Then by re-multiplying by this matrix (of transition) we will not be able to find the state extension (finally the prediction of the state ) n + 1.

What does it look like in Python?

We could calculate matrix multiplications by hand (with numpy for example) and manage the transitions quite simply. The great thing about Python is that there are libraries for everything. Why bother then?

I will import the marc library which will do all the work that we have seen so far.

pip install marc

Once the library is imported / installed, we only have to describe our sequence earlier:

from marc import MarkovChain
import pandas as pd
sequence = [
    'D', 'A', 'A', 
    'A', 'C', 'C',
    'C', 'A', 'A'
]
chaine = MarkovChain(sequence)

The sequence is described in a Python list called a sequence. The call to the MarkovChain () function allows you to do all the calculations we have seen previously.

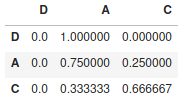
The matrix is ​​calculated, it only remains to display it:

chaine.matrix

[[0.0, 1.0, 0.0],
 [0.0, 0.75, 0.25],
 [0.0, 0.3333333333333333, 0.6666666666666666]]

Of course the library does not stop there, you can calculate the next (probable) step:

chaine.next('A')

'A'

And why not the next 20 …

chaine.next('D', n=20)

['A',
 'A',
 'A',
 'A',
 'A',
 'A',
 'A',
 'A',
 'A',
 'A',
 'C',
 'C',
 'C',
 'A',
 'C',
 'C',
 'C',
 'A',
 'A',
 'C']

Conclusion

Markov chains are in fact not young (Andrei Markov published the first results on Markov chains in 1906) but nevertheless remain very relevant when we have to deal with stochastic processes. Personally, I find them very simple and sometimes even complementary to classic Machine Learning algorithms (decision trees, boost, bayes, etc.). In fact, the fields of application are multiple: writing text or music, weather forecasts, etc.

In short, an algorithm that should not be put aside even if it may seem a little old-fashioned! You need an algorithm that allows you following one sequence of actions to predict the next … take a look at this Algorithm!